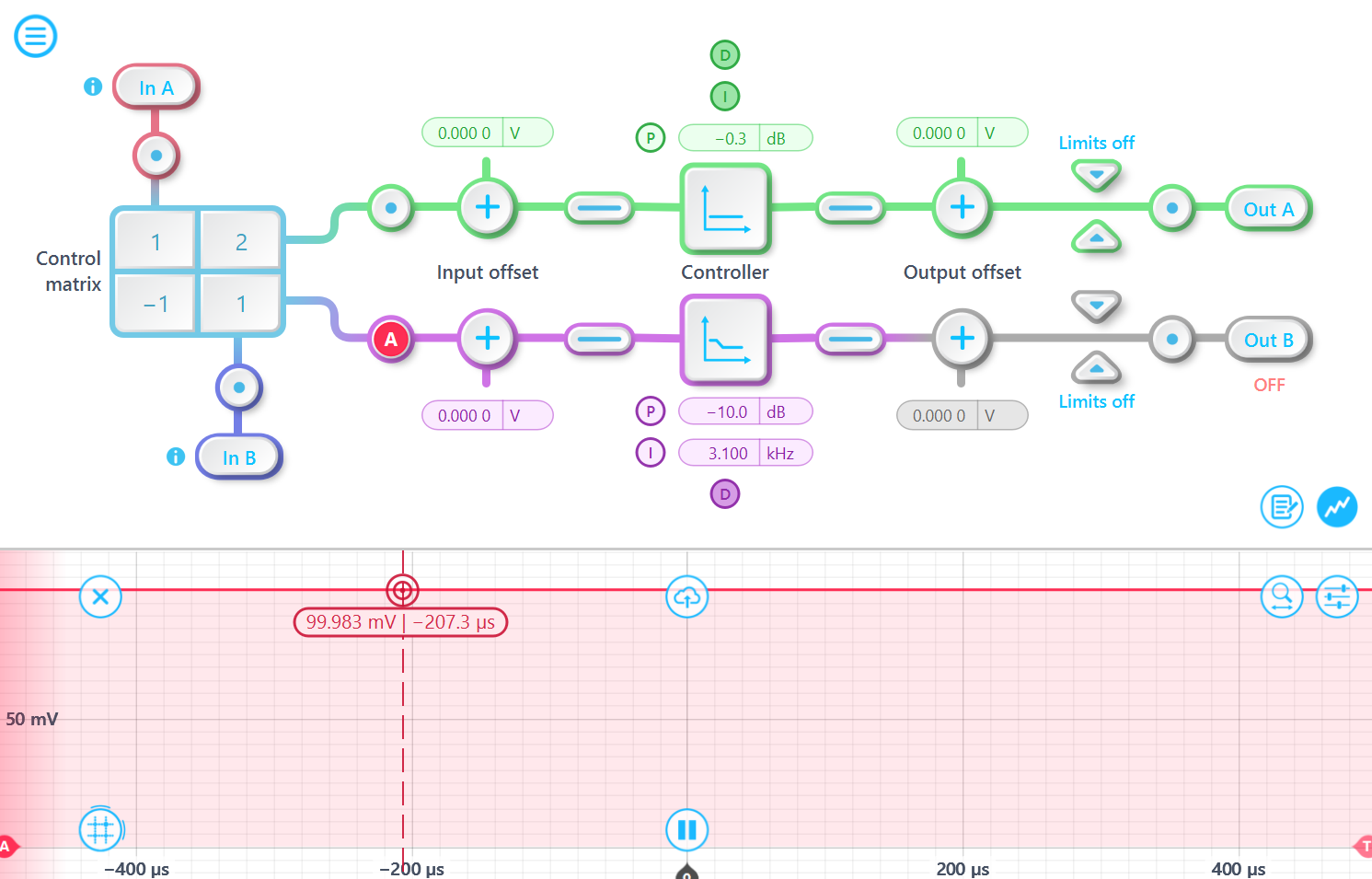
How does the PID control matrix work?
Written by Paul Cracknell
Updated at July 17th, 2024
-
Moku:Go
Moku:Go Arbitrary Waveform Generator Moku:Go Data Logger Moku:Go Frequency Response Analyzer Moku:Go Logic Analyzer & Pattern Generator Moku:Go Oscilloscope & Voltmeter Moku:Go PID Controller Moku:Go Spectrum Analyzer Moku:Go Waveform Generator Moku:Go Power Supplies Moku:Go Digital Filter Box Moku:Go FIR Filter Builder Moku:Go Lock-in Amplifier Moku:Go General Moku:Go Logic Analyzer/Pattern Generator Moku:Go Time & Frequency Analyzer Moku:Go Laser Lock Box Moku:Go Phasemeter
-
Moku:Lab
Moku:Lab General Moku:Lab Arbitrary Waveform Generator Moku:Lab Data Logger Moku:Lab Digital Filter Box Moku:Lab FIR Filter Builder Moku:Lab Frequency Response Analyzer Moku:Lab Laser Lock Box Moku:Lab Lock-in Amplifier Moku:Lab Oscilloscope Moku:Lab Phasemeter Moku:Lab PID Controller Moku:Lab Spectrum Analyzer Moku:Lab Waveform Generator Moku:Lab Time & Frequency Analyzer Moku:Lab Logic Analyzer/Pattern Generator
-
Moku:Pro
Moku:Pro Arbitrary Waveform Generator Moku:Pro Data Logger Moku:Pro Frequency Response Analyzer Moku:Pro Oscilloscope Moku:Pro PID Controller Moku:Pro Spectrum Analyzer Moku:Pro Waveform Generator Moku:Pro Lock-in Amplifier Moku:Pro Digital Filter Box Moku:Pro FIR Filter Builder Moku:Pro Phasemeter Moku:Pro Multi-instrument Mode Moku:Pro General Moku:Pro Logic Analyzer/Pattern Generator Moku:Pro Time & Frequency Analyzer
- Python API
- MATLAB API
- Arbitrary Waveform Generator
- Data Logger
- Digital Filter Box
- FIR Filter Builder
- Frequency Response Analyzer
- Laser Lock Box
- Lock-in Amplifier
- Oscilloscope
- Phasemeter
- PID Controller
- Spectrum Analyzer
- Time & Frequency Analyzer
- Waveform Generator
- Logic Analyzer & Pattern Generator
- Multi Instrument Mode
- Moku Cloud Compile
- Moku general
- LabVIEW
The control matrix combines, rescales, and redistributes the input signal to the two independent PID controllers, FIR filters or digital filters. The output vector is the product of the control matrix multiplied by the input vector.
For instance, in this configuration, the two inputs are DC signals of 50 mV and 150 mV.
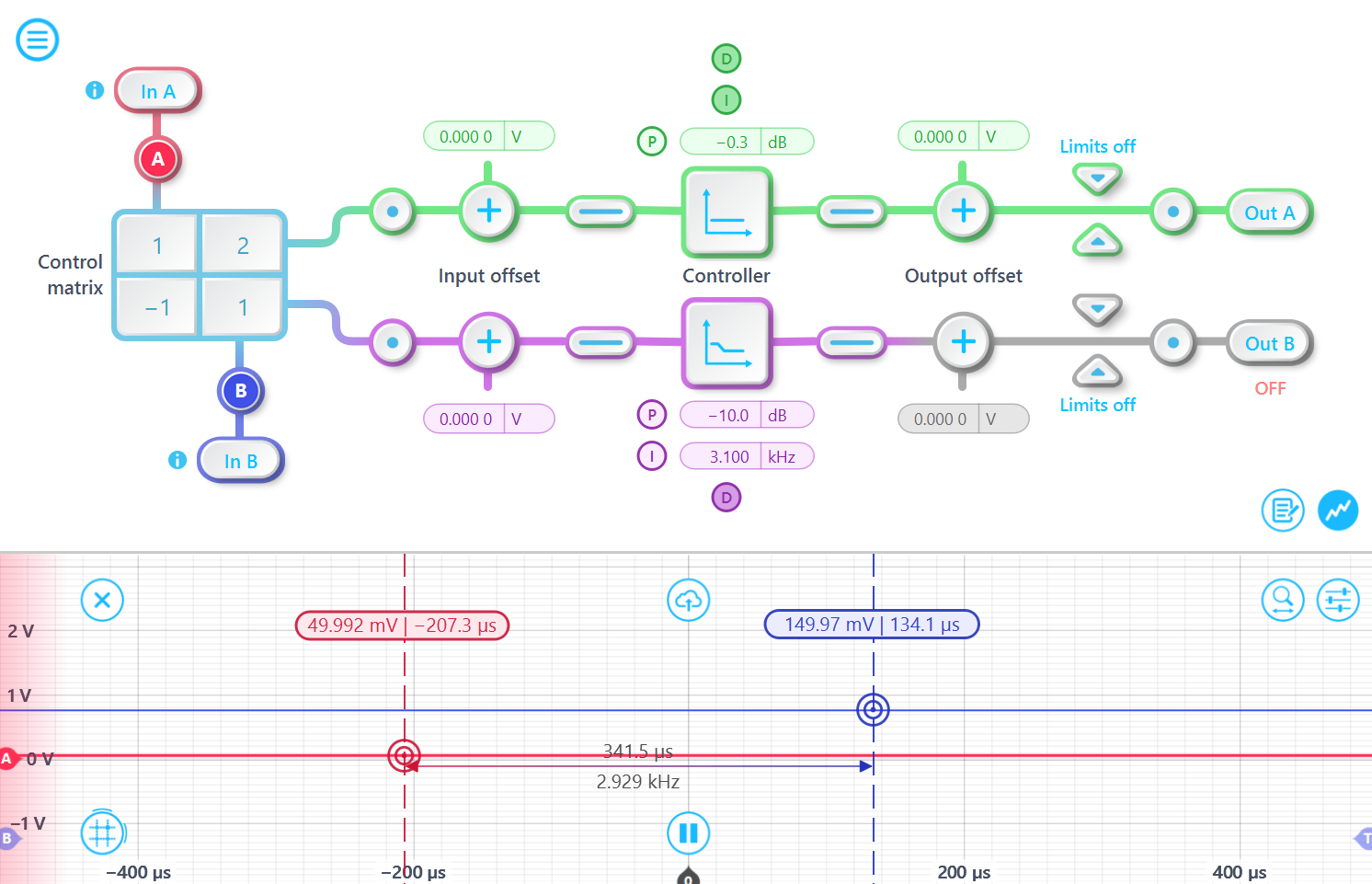
Since the first row of the Control matrix is [1, 2], the ChannelA output of the Control matrix is calculated as 1× InA + 2 × InB = 350 mV.
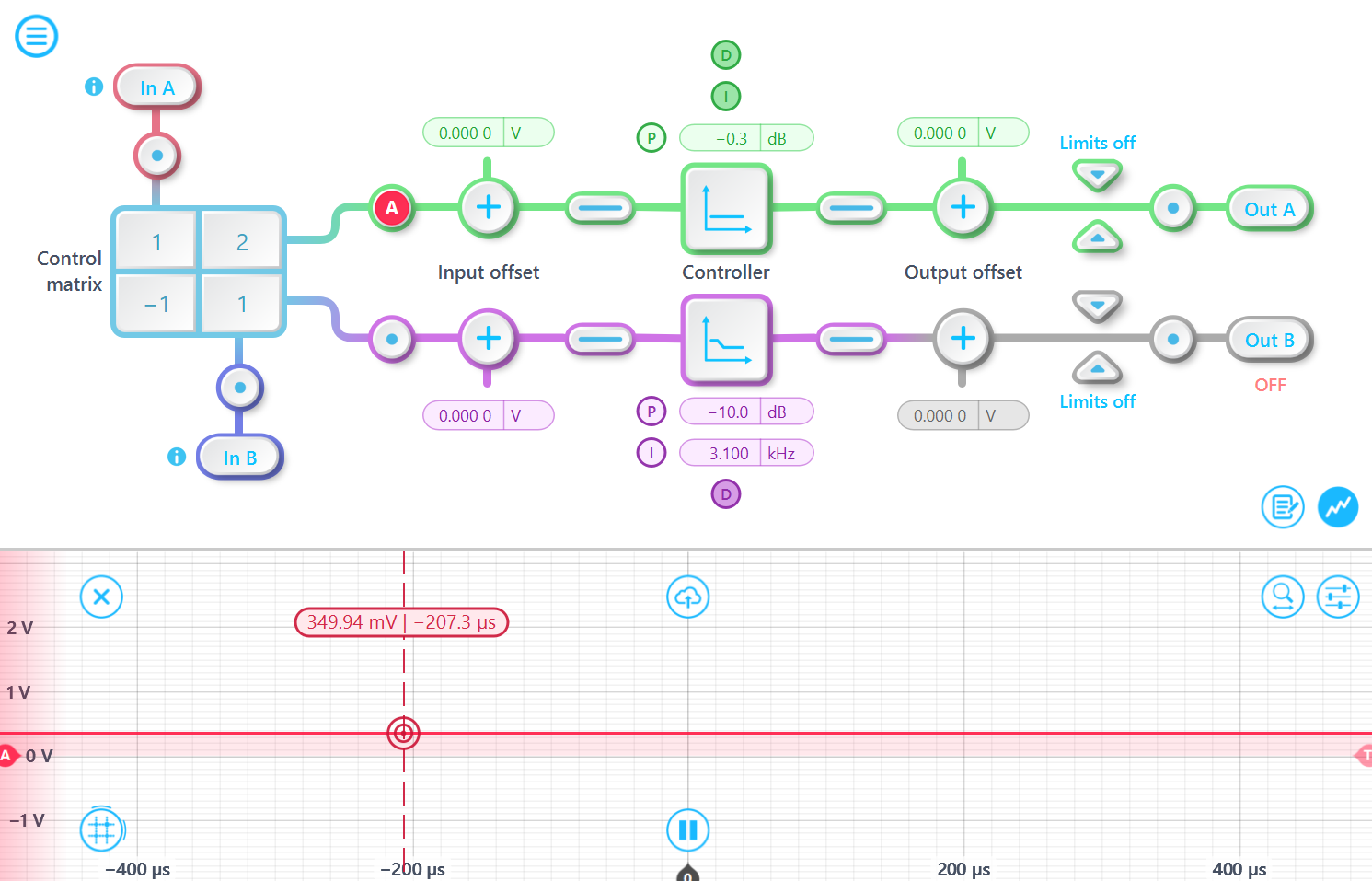
The second row of the Control matrix is [-1, 1], so the ChannelB output of the Control matrix is calculated as -1 × InA + 1 × InB = 100 mV.
